According to de-Broglie a moving material particle sometimes acts as a wave and sometimes as a particle.The waves associated with moving particle is called matter waves or de-Broglie wave and it propagates in the form of wave packets with group velocity.
de-broglie-wavelength
According to de-Broglie theory, the wavelength of de-Broglie wave is given by De-Broglie wavelength, λ=h/mv; where h = Plank's constant, m = Mass of the particle, v = Speed of the particle.
- The smallest wavelength whose measurement is possible is that of γ-rays.
- The wavelength of matter waves associated with the microscopic particles like electron, proton, neutron,α-particle etc. is of the order of m.
De-Broglie wavelength associated with the charged particles
The energy of a charged particle accelerated through potential difference V is
E = 1/2 mv2 = q(pd)
Hence De-Broglie wavelength
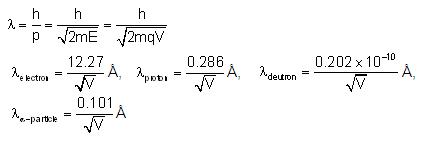
De-Broglie wavelength associated with uncharged particles
For Neutron De-Broglie wavelength is given as
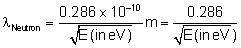 Å
Å
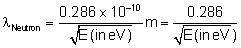 Å
ÅEnergy of thermal neutrons at ordinary temperature 3/2kT; where k = Boltzman's constant = 1.38 x 10-23 Joules/kelvin, T = Absolute temp.
So 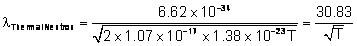 Å
Å
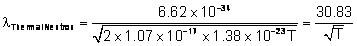 Å
Å
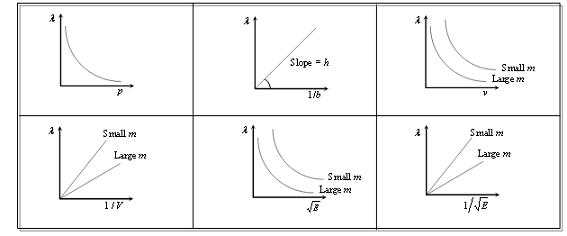
Some Important Graphs:
Characteristics of matter waves:
- Matter waves are not electromagnetic in nature.
- Practical observation of matter waves is possible only when the de-Broglie wavelength is of the order of the size of the particles is nature.
- Electron microscope works on the basis of de-Broglie waves.
- The phase velocity of the matter waves can be greater than the speed of the light.
- The number of de-Broglie waves associated with nth orbital electron is n.
- Only those circular orbits around the nucleus are stable whose circumference is integral multiple of de-Broglie wavelength associated with the orbital electron.

